Artikel
Beobachtungsberichte
Equipment
Literatur
Objektliste
Links
Das bin ich
Impressum
|
Home Artikel Beobachtungsberichte Equipment Literatur |
 |
Projekte Objektliste Links Das bin ich Impressum |
Die Zentralabschattung im Strahlengang eines Newton-Teleskops hat natürlich einen Einfluß auf die Abbildung im Teleskop. Daher will ich die Auswirkung der Obstruktion einmal betrachten.
Konkret geht es bei der Betrachtung um Beugungseffekte, die durch das Teleskop und durch den Fangspiegel verursacht werden.
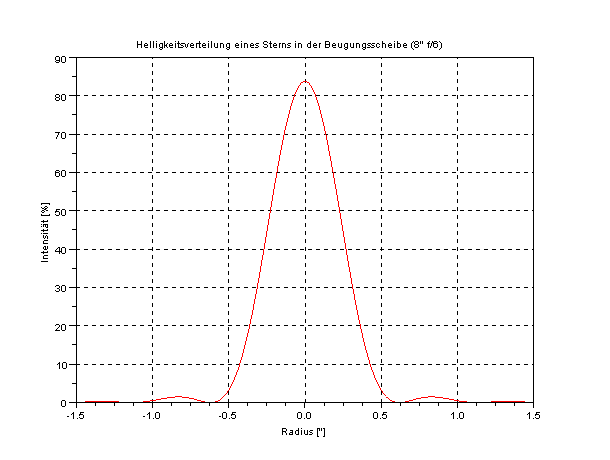
Wenn Lichtstrahlen durch eine (kreisrunde) Öffnung gehen, dann werden diese gebeugt. Das hat zur Folge, das parallel einfallende Strahlen nicht mehr parallel weiterlaufen, sondern andersartig weiterlaufen. Somit entsteht das berühmte Beugungsscheibchen aus einem Stern, obwohl der Stern an sich ja eine Punktlichtquelle ist (und eigentlich als Punkt wieder abgebildet werden soll). Die Helligkeitsverteilung im Beugungsscheibchen in Abhängigkeit vom Abstand von der Achse sieht dann so aus:
[Abbildung 1]
Man sieht, das die (Haupt-)Helligkeit sich auf grob einen Bereich von 1 Bogensekunde verteilt (bis +/-0,5"). Weiterhin wird ein Teil des Lichts in einem zweiten Bereich/Ring (mehr oder weniger deutlich) sichtbar (so etwa bei +/-0,75"), und sogar noch in einem dritten Bereich (so etwa bei +/-1,3"). Das Diagramm stellt eine Beugungsscheibe für ein ideales 8" f/6 Teleskop (ohne einen Fangspiegel) dar. Diese Helligkeitsverteilung einer Punktlichtquelle (also durch einen Stern) entsteht durch die Öffnung (das runde Loch vorne) des Teleskops (ob man das will oder nicht).
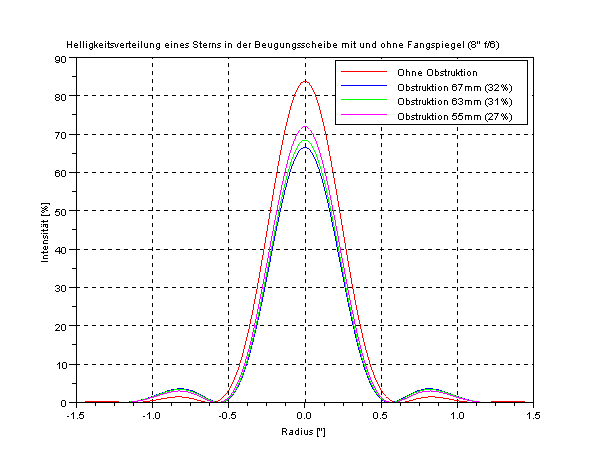
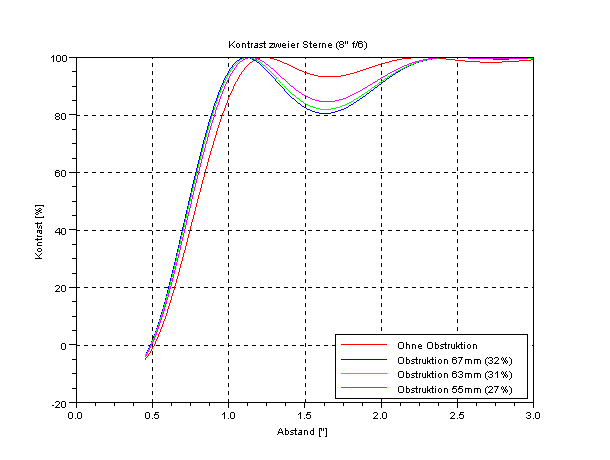
Kommt jetzt noch ein Fangspiegel in die Mitte des Strahlengangs, so ruft dieser natürlich weitere Beugungserscheinungen hervor.
[Abbildung 2]
Wie im Diagramm zu sehen, wird hauptsächlich durch die weitere, durch den Fangspiegel hervorgerufene, Beugung die Lichtmenge im zentralen Scheibchen reduziert und verteilt sich auf die weiter außen liegenden Beugungsringe. Im Diagramm sind einige 8" f/6 Teleskope mit Fangspiegelgrößen von 67mm, 63mm und 55mm dargestellt.
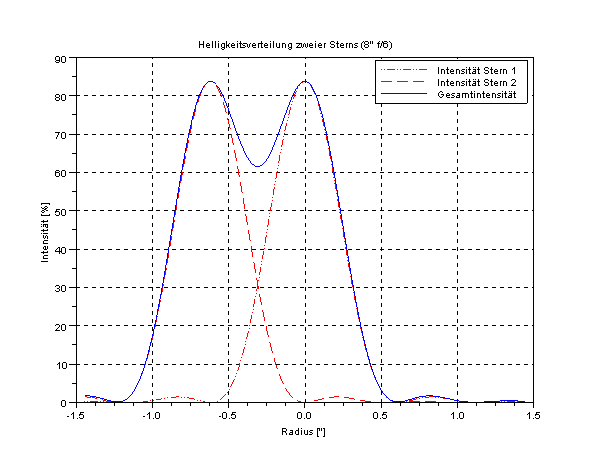
Nun kann man diese Helligkeitsverteilung eines Sterns, hervorgerufen durch den Aufbau des Teleskops, sich für zwei nahe beieinanderliegende Sterne anschauen:
[Abbildung 3]
Die roten Linien im Diagramm sind stellen die Helligkeitsverteilung zweier Sterne dar, die etwa einen Abstand von 0,6" haben. Die blaue Linie ist die Summe der Helligkeiten aus beiden Sternen. Diesen blauen Helligkeitsverlauf sieht man so im Teleskop. Man sieht, das die Helligkeit im Zwischenraum zwischen den beiden Sternen nicht auf Null abfällt, sondern relativ weit oben bleibt. Durch diesen Verlauf sieht man deutlich, das das Trennen der beiden Sterne immer schwieriger wird, je enger diese beisammen liegen. Dieses Problem des Trennens der beiden Sterne ist einzig durch die Beugung hervorgerufen.
Um also die Sterne getrennt sehen zu können, muss im Zwischenraum zwischen den beiden Sternen die Helligkeit entsprechend abfallen, um die Trennung wahrzunehmen. Dieser Helligkeitsunterschied wird als Kontrast betrachtet.
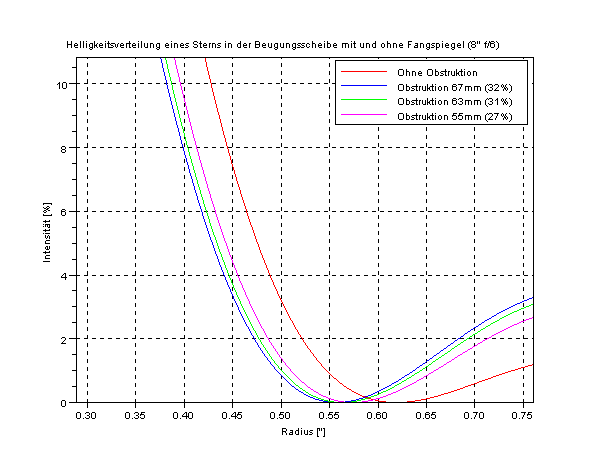
Allgemein wird der Kontrast K folgendermaßen definiert:
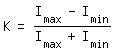
[Gleichung 1]
In unserem Fall/Diagramm ist ist dann die maximale Intensität I(max) die summierte Helligkeit (also die blaue Linie) bei 0". Die minimale Intensität I(min) ist an dem untersten Punkt der blauen Linie zwischen den beiden Sternen. Damit kann man direkt den Kontrast bestimmen, der im Teleskop z.B. zwischen den beiden Sternen in dem Abstand von ca. 0,6" ist.
Diese Betrachtung des Kontrasts kann man im Anschluß dann dahin ausdehnen, das man die beiden Sterne in verschiedenen Abständen betrachtet und für jeden dieser Abstände jeweils den Kontrast bestimmt. Das kann man dann für die verschiedenen Teleskope (oder nur für das eigene) durchführen. Diese Zahlen kann man dann einfach in einem Diagramm auftragen. Als x-Achse nimmt man dann den Abstand der beiden Sterne, als y-Achse den so bestimmten Kontrast.
Das ganze sieht dann folgendermaßen aus:
[Abbildung 4]
Angefangen von einem Abstand von ca. 0,6" steigt allgemein der Kontrast steil an, bis er auf 100% kommt. Anschließend bei etwa 1,6" fällt der Kontrast nochmal leicht ab, um dann zielstrebig zu den 100% zu pendeln. Das unobstruierte Teleskop (rote Linie) hat im linken Bereich (bis ca 1,2") einen niedrigeren Kontrast als die Teleskope mit Fangspiegel. Die anschließende Absenkung ist dafür nicht so stark ausgeprägt.
Aber halt, das unobstruierte Teleskop hat einen niedrigeren Kontrast? Tja, so ist es erst einmal. Dieses Verhalten kann man auch erklären und sehen, wenn man sich die Abbildung 2 genauer schaut. Man sieht, das bei obstruierten Teleskopen mit steigender Fangspiegelgröße die zentrale Beugungsscheibe immer kleiner wird. Deutlicher sichtbar wird dies, wenn man die Abbildung 2 in diesem Bereich etwas vergrößert darstellt:
[Abbildung 5]
Ein Paar Anmerkungen möchte ich zu den Ausführungen noch machen. Zum einen, damit die Diagramme klarer werden, einiges zu den zu Grunde liegenden Formeln. Für die in Abbildung 1 und Abbildung 2 dargestellte Kurve des Helligkeitsverteilung eines Sterns in der Beugungsscheibe benutze ich die Formel
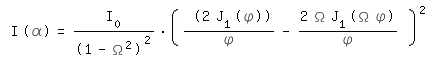
[Gleichung 2]
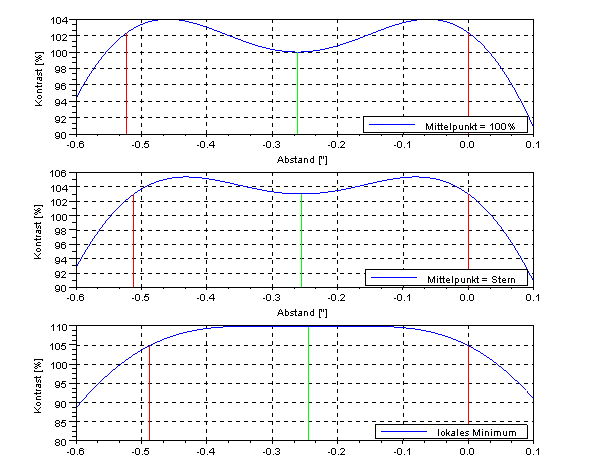
Hierin ist I(α) die Helligkeit im Winkelabstand α (alpha) von der optischen Achse. I0 ist die Maximalhelligkeit, die in der Mitte der Kurve erreicht wird. Die Formel ist normiert, so das (bei I0=1) ein Wert von 1 herauskommt. In dem Diagramm ist weiterhin berücksichtigt, das die Maximalhelligkeit nur einen Wert von etwa 83,3% (vom Sternenlicht) erreicht. Ω (Omega) ist die Obstruktion d/D (Durchmesser Fangspiegel / Durchmesser Hauptspiegel). J1 ist die einfach Bessel-Funktion erster Art. Die Variable φ (phi) ist eine Zwischengröße und wird bestimmt aus:
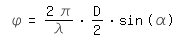
[Gleichung 3]
λ ist die Wellenlänge (ich hab 500nm gewählt), D ist der Durchmesser des Hauptspiegels und α der Winkelabstand von der optischen Achse.
Mit diesen beiden Formeln hab ich dann über den relevanten Bereich (+/-1,5") die Werte ausgerechnet und die Diagramme dargestellt. Solch ein Diagramm nennt man auch Point Spread Funktion (PSF).
Zum Kontrast ist ja die allgemeine Formel schon oben angegeben. Hierbei sind einige Randbedingungen zu beachten, die ich mal erklären möchte. Es geht darum, wo der Kontrast gegen Null geht. Man kann das dann mal so ansetzen, das die Beule zwischen den beiden Sternen einen Wert von I0 (100%) erreicht. Hierbei ist es aber durch die Summe der beiden Helligkeiten der Sterne so, das der Helligkeitswert an der Stelle der beiden Sterne etwas angewachsen ist. Dadurch ist die Beule immer noch, aber nicht mehr so deutlich, vorhanden. Ein anderer Ansatz ist es, das die Beule so hoch wie die Helligkeit an der Stelle der Sterne sein soll. Auch hier ist es durch die Summe der Helligkeiten so, das zwischen einem Stern und dem Mittelpunkt der Helligkeitswert höher als der Helligkeitswert des Sterns ist, also auch so eine kleine Beule vorhanden ist. Ein nächster Ansatz ist es, das das lokale Minimum (also die nach unten gerichtete Beule) in ein Maximum wechselt. Damit ist keine Beule (nach unten) mehr vorhanden. In der folgenden Grafik hab ich versucht, diese drei unterschiedlichen Ansätze mal darzustellen:
[Abbildung 6]
Alle drei Ansätze sind korrekt und haben ihre Daseinsberechtigung. Für die weitere Betrachtung ist dieser feine Unterschied jedoch nicht so relevant. Ich werde den zweiten Ansatz (Helligkeit Beule gleich Helligkeit Stern) benutzen.
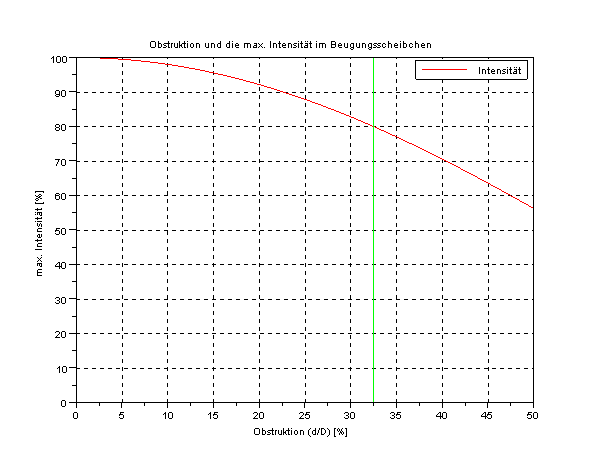
Eine kleine Anmerkung gibts noch zu diesen Diagrammen. In der Abbildung 2 sieht man, das bei steigender Obstruktion das Maximum in der Mitte der Kurven immer weiter sinkt. Erinnern wir uns an den Begriff Strehl. Der Strehlwert gibt das Verhältnis der maximale Intensität eines realen optischen Systems zu der maximalen Intensität eines idealen optischen Systems an.
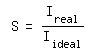
[Gleichung 4]
Aus der Gleichung 2 sieht man (die ja normiert ist), das über den Obstruktionsterm die maximale Intensität in Abhängigkeit der Obstuktion direkt bestimmt werden kann.
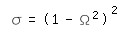
[Gleichung 5]
Stelle ich nun das Verhaltnis der maximalen, realen Intensität zur maximalen, idealen Intensität dar:
[Abbildung 7]
Hier sieht man, das die maximale Intensität mit steigender Obstruktion immer weiter fällt. Zieht man nun wieder den Strehlwert und die daraus übliche Definition der beugungsbegrenzten Abbildung (S>0,8) heran, so kann man die Auswirkung der Obstruktion auf eine beugungsbegrenzte Abbildung in der Grafik ablesen. Diese Grenze hab ich grün eingezeichnet. Wer es genauer haben will, kann dies auch berechnen:
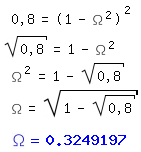
[Gleichung 6]
Kurz und bündig als Ergebnis heißt das, das ab einer Obstruktion von ca. 33% rein physikalisch keine beugungsbegrenze Abbildung mehr möglich ist. Hierbei sind nicht einmal weitere abbildungsverschlechternde Effekte berücksichtigt, sondern rein die Auswirkung der Obstruktion. Kommen, was ja natürlich ist, weitere Abbildungsfehler dazu, so muß der Fangspiegel/die Obstruktion noch einiges kleiner werden, damit das Gesamtsystem beugungsbegrenzt abbildet.
Und wer fragt sich nun nicht selbst, ob sein eigenes Gerät noch beugungsbegrenzt ist...
Bevor es richtig weitergeht, möchte ich zuerst ein wenig ausholen.
Wenn man aus einer Point Spread Function (PSF) eine Modulation Transfer Function (MTF) berechnet, kommt ein mathematisches Werkzeug zum Einsatz, welches ich erst ein wenig erläutern möchte (ohne in die Tiefen oder Feinheiten einzusteigen). Der ein oder andere hat bestimmt schon einmal gehört, das man mit einer Überlagerung von Kosinus- (oder auch Sinus-) Schwingungen ein beliebiges Signal nachbilden kann. Bei dieser Überlagerung summiert man die Funktionswerte der Kosinus-Funktion mit unterschiedlichen Frequenzen auf. Meist erfolgen diese Frequenzenangaben ω (Omega) dann über n*ω mit ω = 2*π*f(basis) und n einer natürlichen Zahl (1, 2, 3, ...). Hierbei ist f(basis) die Basisfrequenz und π (Pi) die Kreiszahl. Man addiert also salopp gesagt cos(1*ω*x)+cos(2*ω*x)+cos(3*ω*x)+... auf. Etwas genauer gilt dann:
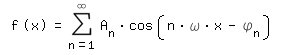
[Gleichung 7]
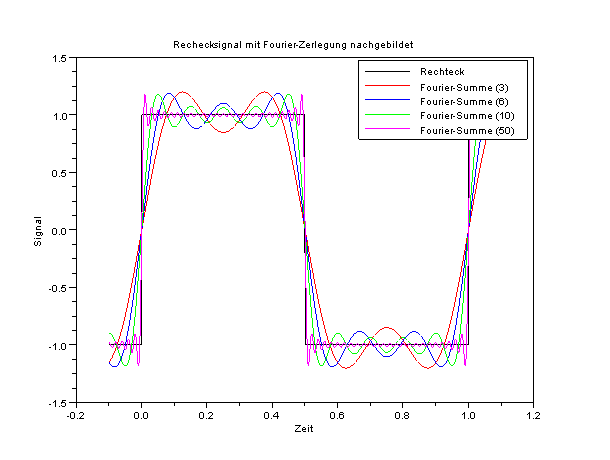
Für ein Rechtecksignal, welches über diese Kosinus-Summen erzeugt wird, sieht das dann folgendermaßen aus:
[Abbildung 8]
Das Rechtecksignal (schwarz) wird über verschieden viele Kosinus-Summen erzeugt. Je mehr Summanden man benutzt, um so genauer wird der Rechteck nachgebildet. Geht man dabei bis zu unendlich vielen Summanden, so wird das Signal sehr genau nachgebildet. In der Realität schätzt man ab, bis zu welchem Summanden das Signal hnreichend genau beschrieben wird (um nicht mit unendlich vielen Summanden rechnen zu müssen).
Umgekehrt kann man auch ein Signal in die einzelnen Kosinus-Teile zerlegen. Das entsprechende Werkzeug dazu heißt Fourier-Zerlegung. Man berechnet damit die einzelnen Frequenzen (das mit dem ω), mit denen die Kosinus-Summe zu bilden ist. Weiterhin erhält man die Amplituden der Frequenzen sowie die Winkel der Verschiebung der Kosinus-Funktion bei den Frequenzen.
Unser Signal ist in diesem Fall die Point Spread Funktion (PSF). Aus dieser werden diese Kosinus-Anteile mit der Fourier-Zerlegung bestimmt. Als Ergebnis hat man dann die Amplituden und die Verschiebungen bei verschiedenen Frequenzen, also konkret die Frequenzanteile der Point Spread Funktion.
Für die Modulation Transfer Function (MTF) trägt man also die Amplituden über die Frequenzen auf. Um nun eine Vergleichbarkeit des Kurvenverlaufs zu haben, wird meist auf die Maximalfrequenz und auf die Maximalamplitude normiert. Diese Normierung führt eigentlich nur dazu, das die Amplitudenwerte von 0%..100% und die Frequenzwerte von 0..1 gehen.
Eine solche Zerlegung hab ich mal gemacht und die Werte frequenzmäßig auf 0-Kontrast normiert, die Amplituden sind auf die 0%..100% normiert. Das Ganze sieht dann folgendermaßen aus:
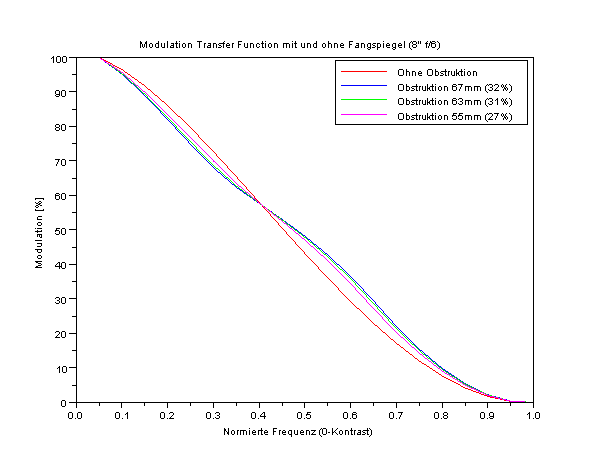
[Abbildung 9]
Das war jetzt im Schnellverfahren die Berechnung der Modulation Transfer Function (MTF).
Von links nach rechts fällt die Kurve von 100% auf 0% ab. Links ist die Frequenz 0 und rechts die Frequenz 1. Diese Frequenz 1 (rechts) ist die normierte Freuqenz, also die maximale Frequenz. Als Frequenz ist hier die Auflösungsfrequenz zu verstehen, die mit kleiner werdender Auflösung im Teleskop immer größer wird (wegen allgemein f = 1/T mit T dann als Auflösung). Bis zur etwa knapp halben Maximalfrequenz ist links der Kontrast der obstruierten Teleskope geringer als die eines unobstruierten Teleskops. Rechts von dem Übergang ist der Kontrast der obstruierten Teleskope größer als die des unobstruierten Teleskops (das Verhalten haben wir auch schon in Abbildung 4 gesehen).
Bevor weitere Diagramme hier dargestellt werden, will ich noch schnell ein Par weitere Worte über das Modulation Transfer Function Diagramm (Abbildung 9) verlieren, um so das Diagramm (halbwegs) lesen zu können. Dazu fang ich mal bei der x-Achse (auch Abszisse) an, diese stellt ja die normierte Frequenz dar. Mit der Normierung wird der Maximalwert ja zu 1.
Und was bedeutet diese 1? Dazu muss man sich schon genau anschauen, auf was da normiert wurde. Ich hab da 0-Kontrast dazu hingeschrieben. Das heißt also, ich hab als maximale Frequenz (also 1 durch Auflösung) die Frequenz/Auflösung genommen, bei der der Kontrast gegen 0 geht. Diese 0-Kontrast-Auflösung liegt bei etwa einer halben Bogensekunde. Diese Auflösung ist, um es klarzustellen, nicht die Auflösung nach Rayleigh (mit 500mn und 8" sind es 0,63"). Diese Auflösung ist definiert mit dem Abstand zweier Sterne, bei dem das erste Minimum des Beugungsscheibchens eines Sterns im Maximum (in der Mitte) des anderen Sterns ist. Hierbei ist der Kontrast folglich nicht null (sieht man auch in Abbildung 3).
Für das dargestellte MTF Diagramm (Abbildung 9) heißt das, das engere Auflösungen im rechten Bereich dargestellt werden als die bei Rayleigh definierte Grenze. Die Rayleigh-Grenze liegt in dem Diagramm bei einer Frequenz von etwa 0,8.
Dann haben wir einen Übergang der farbigen Kurven (von links gesehen) von unterhalb der roten Kurve zu überhalb der roten Kurve bei einer Frequenz von 0,45 (die rote Kurve ist die des unobstruierten Teleskops). Wie gehabt, die 0,45 ist keine echte Frequenz, sondern eine normierte Frequenz. Mit der Maximalauflösung (damit die Frequenz) des Diagramms - wie oben angegeben - von 0,5 Bogensekunden heißt das, der Übergang liegt bei einer Auflösung von 1/0,45 * 0,5", also etwas höher als eine Bogensekunde.
Auf der linken Seite im Diagramm gehen die Kurven alle gegen 100%. Da links ja die niedrige Auflösung ist, ist der Kontrast bei großen Abständen bei allen Teleskopen bei 100%, also optimal. Rechts im Diagramm ist die Grenzauflösung, bei der alle Kurven gegen 0% gehen. Weiter rechts (außerhalb des Diagramms) wäre der Bereich, in dem alle Teleskope feinere Details nicht mehr auflösen können. Daher wird das Diagramm auch da abgeschnitten. Einzig der Bereich dazwischen von etwa 0,1*Grenzfrequenz bis zur Grenzfrequenz ist relevant und hierin unterscheiden sich die Kurven und damit die Teleskope.
Fang ich mal mit den visuellen Deep-Sky Jüngern an. Man kennt sie mit den großen Dobson, oder sollten die lieber zu einer Linse greifen?
Die Ausleuchtung des Feldes ist ist zwar ein Aspekt, der nicht ganz vernachlässigt werden soll (zur Vignettierung hatte astrobart ja schon einen Link geschickt). Aber es darf visuell m.E auch nicht überbewertet werden. Auch mit einem nicht voll ausgeleuteten Feld sieht man schon alles. Und da die großen Objekte, die evtl. nicht voll ausgeleuchtet werden, i.d.R. [i]abgefahren[/i] werden, macht die Vignettierung auch nicht die Bohne aus.
Schauen wir und als nächstes das MTF-Diagramm (Abbildung 9) an. Im linken Bereich liegt der Kontrast der obstruierten Teleskope unter dem der - ich sag mal salopp - Linsenteleskope, im rechten Bereich ist der Kontrast über dem der Linsenteleskope (Linse=rote Kurve). Die Grenze liegt bei etwa einer Bogensekunde. Da visuell beobachtet wird, muss man auch berücksichtigen, das das Seeing in dieser Größenordnung liegt. Das heißt auch, das der rechte Teil des MTF-Diagramms für die visuelle Beobachtung eigentlich völlig irrelevant ist. Und aus dem linken Teil geht klar hervor, das die Linse dem Spiegel überlegen ist.
Aber beim Deep-Sky-Beobachten kommt es auch auf das Lichtsammeln an. Wäre die Herstellung und der Bau eines großen, viel Licht sammelnden Linsenteleskops aber genauso einfach wie ein Newton-Teleskop mit Fangspiegel, dann wäre die Linse wohl das meistbenutzte visuelle Deep-Sky Teleskop. Da die Größe der Linse schwer zu schaffen macht und der Bau der Spiegelteleskope die Größe ohne weiteres zulassen, ist das Dobson Teleskop wohl das meistbenutzte Teleskop.
Nun zu den visuellen Mond- und Planeten Jüngern. Es sieht mit der Ausleuchtung ähnlich aus wie bei den anderen Visuellen, also nicht so wichtig ist. Hinzu kommt, das die Planeten ja auch relativ klein sind und das Feld drumherum nicht Ziel der Beobachtung darstellt. Und auch am Mond kann man spazieren gehen, also hin und herschwenken.
Da aber auch die Lichtsammelleistung nebensächlich ist (von dem Mond und den Planeten kommt genügend Licht), muss das Teleskop auch nicht so groß sein. Daher ist auch nicht die Einschränkung der Baugröße ein Problem. Ein kleineres (aber qualitativ hochwertiges) Linsenteleskop kann schon echt entzücken, und die MTF sagt eine doch schon bessere Abbildung voraus. Insgesamt hat also die Linse im Vergleich zum (gleichgroßen) Spiegel einfach die Nase vorne. Klar aber auch, das das größere (und i.d.R. auch billigerere) Spiegeleteleskop der kleinen Linse den Rang ablaufen kann.
Die Ausleuchtung ist bei den Deep-Sky-Fotografen ein wichtiger Aspekt (denn auch die Ästhetik des Bildes spielt meist eine große Rolle). Daher sollte diese Gattung auch mehr auf die Ausleuchtung achen. Da Lichtsammelleistung aber auch hier durch längere Belichtung erfolgen kann (und auch hier die Seeing-Grenze beachtet werden muss), kann auch ein kleineres Linsenteleskop hervorraugende Dienste leisten. Ausleuchtung ist dann aufgrund des (im Linsenteleskop nicht vohandenen) Fangspiegels nicht so das Problem. Das MTF-Diagramm im linken Bereich spricht jedenfalls für die Linse und die Baugröße kann kompensiert werden. Man beachte, das auch größere Spiegelteleskope entsprechend montiert werden müssen.
Einen Kompromiss bei der Ausleuchtung kann man mit einem (etwas größeren) Spiegeltelekop auch eingehen, wenn man sich auf das Objekt und nicht auf das Feld drumerum (also das Gesamtbild) konzentriert. Will man (nur) eine Galaxie ablichen, dann sollte auch nur diese Galaxie ausgeleuchtet sein, ansonsten verschenkt man Informationen im Objekt. Ist dies das Ziel (und nicht das Gesamtwerk), so kann ein etwas größerer Newton (gegenüber dem Linsenteleskop) eingesetzt werden, und ein kleinerer Fangspiegel die Abbildungsqualität etwas verbessern (gegenüber einem voll ausgeleuchteten Bildfeld).
Planetenbilder entstehen heute meist mit der Webcam. Kurze Belichtungen, viele Bilder, und dann die besten Bilder heraussuchen und ein Summenbild stacken. Da sehr kurz belichtet wird, wird die Seeinggrenze ausgehebelt. Und die Lucky Pictures, bei denen das gelingt, kommen in die Weiterwerarbeitung. Damit kommt man in dem MTF-Diagramm auch endlich mal in den rechten Bereich. Genau da hat dann ein obstruiertes Teleskop bei kleinen, kontrastreichen Details (wie z.B. die Saturnringe) die Nase vorne. Ausleuchtung ist, wie oben gesagt, kein Problem. Und ein größerer Fangspiegel kann da schon noch ein bisschen herauskitzeln, was den Linsenteleskopen dann nicht mehr gelingt.
Das soll es erst mal an Zusammenfassung sein, und wie gesagt, das ist so meine Erkenntnis aus dem Thema, bestimmt nicht allumfassend, aber mal ein Anfang...
Stand: 1. Dezember 2010